|
|
|
|
|
|
The Exponential Growth Model and its Symbolic Solution
Thomas Malthus, an 18th century English scholar, observed in an essay written in 1798 that the growth of the human population is fundamentally different from the growth of the food supply to feed that population. He wrote that the human population was growing geometrically [i.e. exponentially] while the food supply was growing arithmetically [i.e. linearly]. He concluded that left unchecked, it would only be a matter of time before the world's population would be too large to feed itself.
The first growth model we examine in this module is the one Thomas Malthus referred to in his famous essay. (In part 3 of this module we will consider a more sophisticated model for the special case of world population). Malthus' model is commonly called the natural growth model or exponential growth model. For this model we assume that the population grows at a rate that is proportional to itself. If P represents such population then the assumption of natural growth can be written symbolically as
where k is a positive constant.
This model has many applications besides population growth. For example, the balance in a savings account with interest compounded continuously (and no withdrawals) exhibits natural growth. In this case, the constant k is called the annual rate of interest. Also, large animal populations whose size is not constrained by environmental factors grow exponentially. In this setting, k is called the productivity rate of the population.
On your worksheet, plot the slope field for the differential equation, and superimpose the solution to the initial value problem for three different values of Q0.
Testing for Exponential Growth
The following table lists the population of the city of Houston, Texas ( county metropolitan statistical area) from the year 1850 to 1980.
| Census Date | Population |
| 1850 | 18,632 |
| 1860 | 35,442 |
| 1870 | 49.986 |
| 1880 | 71,316 |
| 1890 | 86,224 |
| 1900 | 134,600 |
| 1910 | 185,654 |
| 1920 | 272,475 |
| 1930 | 455,570 |
| 1940 | 646,869 |
| 1950 | 947,500 |
| 1960 | 1,430,394 |
| 1970 | 1,999,316 |
| 1980 | 2,905,334 |
"A thousand millions are just as easily doubled every 25 years by the power of population as a thousand. But the food to support the increase from the greater number will by no means be obtained with the same facility".
In other words, Malthus is claiming that, for a population undergoing exponential growth, the time it takes to double is independent of the size of the population.
How long did it take to double again from 70,000 to 140,000?
How long did it take to double from 1 million to 2 million?
Do the doubling times of the Houston population support the assumption of exponential growth?
The tests we carried out on the Houston population data indicate that an exponential model is reasonable. In this section, we discuss ways of finding an exponential function that "fits" the data.
In step 9 you showed that if the plot of the natural log of the population P versus time t is linear, then an exponential function of the form P = P0ekt fits the data. Now we investigate how to use the slope and y-intercept of this line to determine P0 and k.
Now we want to explore another test of data for exponential growth. This test, unlike the previous one, does not use the solution to the differential equation dP/dt = kP, but, instead, checks the differential equation directly.
Our first step will be to approximate dP/dt from our data set. We will do this using symmetric differences, a technique we explain below.
Suppose our data approximates the values of a function P at the points t1, t2, and t3. How can we use the data to approximate the value of dP/dt at t2?
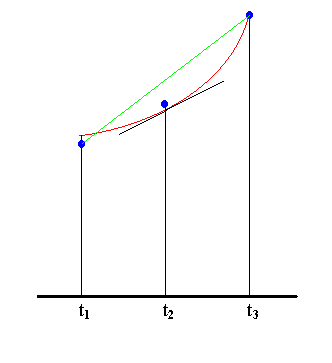
In the above illustration, the three data points which appproximate the values of the function P at t1, t2, and t3 are shown in blue. The graph of P is drawn in red, and the tangent line to the graph of P at t2 is drawn in black. We use the slope of the secant line (in green) which connects the data points at t1 and t3 to estimate dP/dt at t2. This is the symmetric difference approximation to the derivative.
where P1 is the approximate value of P at t1, and P3 is the approximate value of P at t3.
and see whether they are approximately constant.
In later parts of this module we will use symmetric differences on data that is not evenly spaced -- in contrast to the Houston population data, which was given every ten years. Nevertheless, we will use the same method of approximating the derivative and continue to call it a "symmetric difference approximation." So, suppose that our data set contains approximations P1, P2, ..., Pn to the values of a function P(t) at t1, t2, ... ,tn. We will approximate the value of dP/dt at tk (for k not equal to 1 or n) by

|
|
|
| modules at math.duke.edu | Copyright CCP and the author(s), 1999 |